The variational method for geodesics

We now apply the variational technique to compute the geodesics  for a given metric.

For a curved spacetime, the proper time  is defined to be

Remember in flat spacetime  it was just

Therefore the proper time between two points A and B along an arbitrary timelike curve is

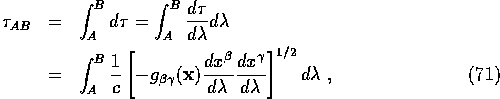
so we can write the Lagrangian  as

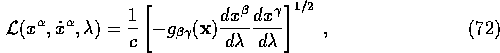
and the action becomes

varying the action  we get the Euler- Lagrange equations :

Now

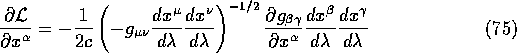
and

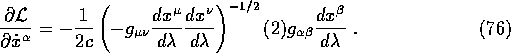
Since

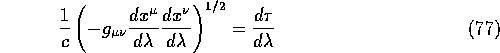
we get

and

so the Euler- Lagrange equations become:

Multiplying by we obtain

Using

we get

Multiplying by gives

Now

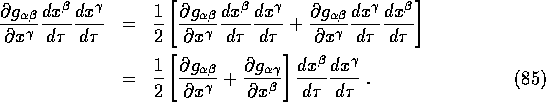
Using the above result gives us

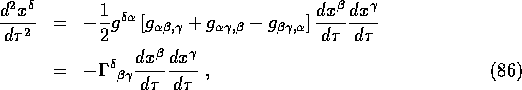
so we get the geodesic equation again 

This is the equation of motion for a particle moving on a timelike geodesic in curved spacetime. Note that in a local inertial frame i.e. where , the equation reduces to

which is the equation of motion for a free particle .

The geodesic equation preserves its form if we parameterize the curve by any other parameter such that

for constants a and b. A parameter which satisfies this condition is said to be affine.